Wat hebben de Pyramide van Giza, Leonardo da Vinci’s Mona Liza en de Aston Martin gemeen? Ze zijn ontworpen volgens ‘De Gulden Snede’. De Gulden Snede, Golden Ratio, Sectio Aurea of Sectio Divina, ook wel de verdeling in uiterste genaamd, is de verdeling van een lijnstuk in twee delen in een speciale verhouding.
Gulden snede
De gulden snede, ook wel bekend als de “gulden verhouding” of “de goddelijke verhouding,” is een wiskundige verhouding, die vaak wordt geassocieerd met esthetische schoonheid en harmonie in kunst, architectuur en natuur. Deze verhouding wordt meestal weergegeven door het getal φ (phi), dat ongeveer gelijk is aan 1,61803.
De gulden snede wordt gedefinieerd als de verhouding tussen twee delen van een object of lijn, waarbij het grotere deel zich verhoudt tot het kleinere deel zoals het gehele deel zich verhoudt tot het grotere deel. Dit kan worden uitgedrukt als: (A + B) / A = A / B = φ
Wiskundig gezien geldt dat de verhouding φ kan worden berekend door de vergelijking φ = (1 + √5) / 2.
Deze verhouding is opmerkelijk vanwege zijn aanwezigheid in de natuur, zoals in de spiraalvormige schelp van een slak, de verdeling van bladeren op een stengel, en de verhouding van de afmetingen van het menselijk lichaam. Het wordt ook veelvuldig toegepast in de kunst en architectuur, waarbij kunstenaars en architecten de gulden snede gebruiken om esthetisch aangename verhoudingen en composities te creëren.
In de geschiedenis hebben beroemde kunstenaars zoals Leonardo da Vinci en architecten zoals Le Corbusier de gulden snede toegepast in hun werken. Het wordt beschouwd als een belangrijk hulpmiddel voor het creëren van visuele harmonie en evenwicht in kunst en design.
Kortom, de gulden snede is een wiskundige verhouding die wordt gewaardeerd om zijn esthetische en harmonische eigenschappen en wordt vaak gebruikt in kunst, architectuur en ontwerp.
Fibonacci
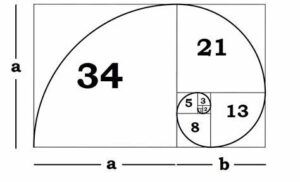
Wiskundigen, wetenschappers en natuuronderzoekers kennen deze verhouding al eeuwen. Het is afgeleid van ‘de Fibonacci-reeks’, genoemd naar zijn Italiaanse oprichter, Leonardo van Pisa, bijgenaamd Fibonacci (van wie de geboorte rond 1175 AD en de dood rond 1250 AD wordt verondersteld). Elke term in deze reeks is eenvoudig de som van de twee voorgaande termen (1, 1, 2, 3, 5, 8, 13, etc.). Fibonacci noemt de rij in zijn boek ‘Liber Abaci’ (boek van de rekenkunst) uit 1202. Een dergelijke reeks wordt reeds genoemd in de Chhandah-shãstra (kunst van de versmaat) van de Sanskriet schrijver Pingala (tussen 200 en 450 v.Chr).
Belangrijkste leerpunten
De Fibonacci-reeks, die in de wiskunde een ‘recursieve definitie’ wordt genoemd, kan worden toegepast met behulp van vier hoofdtechnieken: retracements, bogen, waaierlijnen en tijdzones.
Maar deze volgorde is niet zo belangrijk; het is eerder het quotiënt van de aangrenzende termen, die een verbazingwekkende verhouding hebben, ruwweg 1.618, of zijn omgekeerde 0.618. Deze verhouding is bekend onder vele namen: de gulden snede, de gulden middenweg, PHI en de goddelijke verhouding. Dus waarom is deze reeks zo belangrijk? Bijna alles heeft dimensionale eigenschappen, die zich houden aan de verhouding van 1.618, dus het lijkt een fundamentele functie te hebben voor de bouwstenen van de natuur.
Bewijs
Neem bijvoorbeeld honingbijen. Als je de vrouwelijke bijen deelt door de mannelijke bijen in een bepaalde bijenkorf, krijg je 1.618. Zonnebloemen, die tegengestelde spiralen van zaden hebben, hebben een verhouding van 1,618 tussen de diameters van elke rotatie. Dezelfde verhouding is te zien in relaties tussen verschillende componenten in de natuur.
Nog iets dat gemakkelijk gemeten kan worden? Meet vanaf je schouder tot je vingertoppen en deel dit getal door de lengte van je elleboog tot je vingertoppen. Of probeer te meten van je hoofd tot je voeten, en deel dat door de lengte van je navel tot je voeten. Zijn de resultaten hetzelfde? Ergens in de buurt van 1.618? De gulden snede is schijnbaar onvermijdelijk.
Maar dat betekent niet dat het werkt in de financiële wereld toch? Eigenlijk hebben de markten dezelfde wiskundige basis als deze natuurlijke fenomenen. Hieronder enkele manieren waarop deze ratio kan worden toegepast op financiering,
De Fibonacci onderzoeken en kosten
Bij gebruik in technische analyse wordt de gulden snede meestal vertaald in drie percentages: 38,2%, 50% en 61,8%. Indien nodig kunnen echter meer veelvouden worden gebruikt, zoals 23,6%, 161,8%, 423%, enzovoort. Er zijn vier primaire methoden voor het toepassen van de Fibonacci-reeks om te financieren: retracements , bogen, waaierlijnen en tijdzones.
- Fibonacci-retracements
Fibonacci-retracements gebruiken horizontale lijnen om steun- of weerstandsgebieden aan te geven, waardoor ze nuttig zijn voor handelaren. Ze worden berekend door eerst het hoogste en laagste punt van de grafiek te vinden. Vervolgens worden vijf lijnen getekend: de eerste op 100% (de hoogste op de grafiek), de tweede op 61,8%, de derde op 50%, de vierde op 38,2% en de laatste op 0% (de laagste op de grafiek) ). Na een aanzienlijke prijsbeweging omhoog of omlaag, liggen de nieuwe ondersteunings- en weerstandsniveaus vaak op of nabij deze lijnen. - Fibonacci-bogen
Het vinden van het hoogste en laagste punt van een grafiek is de eerste stap bij het samenstellen van Fibonacci-bogen. Vervolgens worden met een kompasachtige beweging drie gebogen lijnen getekend op 38,2%, 50% en 61,8% vanaf het gewenste punt. Deze lijnen anticiperen op de ondersteunings- en weerstandsniveaus, evenals op bereikgebieden. - Fibonacci-waaierlijnen
Fibonacci-waaierlijnen zijn samengesteld uit diagonale lijnen. Nadat de hoog en laag van de grafiek is gevonden, wordt een onzichtbare verticale lijn door het meest rechtse punt getrokken . Deze onzichtbare lijn wordt vervolgens verdeeld in 38,2%, 50% en 61,8% en lijnen worden vanaf het meest linkse punt door elk van deze punten getrokken. Deze lijnen geven steun- en weerstandsgebieden aan. - Fibonacci-tijdzones
In tegenstelling tot de andere Fibonacci-methoden, zijn tijdzones een reeks verticale lijnen. Ze worden samengesteld door een grafiek te verdelen in segmenten met verticale lijnen op afstand van elkaar in stappen die overeenkomen met de Fibonacci-reeks (1, 1, 2, 3, 5, 8, 13, enz.). Deze lijnen geven gebieden aan waar grote prijsbewegingen kunnen worden verwacht.
Tot slot
De gulden snede kan worden toegepast op alles, van de natuur tot de menselijke anatomie en financieren. Deze Fibonacci-onderzoeken zijn niet bedoeld om de primaire indicaties te geven voor de timing van het begin en einde van aandelen; ze zijn echter nuttig voor het schatten van steun- en weerstandsgebieden. Veel mensen gebruiken combinaties van Fibonacci-onderzoeken om een meer accurate voorspelling te verkrijgen. Een handelaar kan bijvoorbeeld de kruisende punten waarnemen in een combinatie van de Fibonacci-bogen en weerstanden.
Veel meer onderzoekers gebruiken de Fibonacci-onderzoeken in combinatie met andere vormen van technische analyse. De Fibonacci-onderzoeken worden bijvoorbeeld vaak gebruikt met Elliott Golfprincipe. Dit is een vorm van technische analyse, die financiële handelaren gebruiken om financiële marktcycli te analyseren en markttrends te voorspellen.
Wellicht vindt u uw eigen nichegebruik voor de Fibonacci-onderzoeken en voegt u deze toe aan uw set van investeringstools.